İstanbul Ticaret Üniversitesi Elektroniğe giriş dersi Arasınav soruları
Hazırlayan: Şadi Evren ŞEKER
A Grubu Soru 0) Aşağıda verilen devreyi analiz edip her direnç üzerindeki gerilimi ve akımı bulunuz.
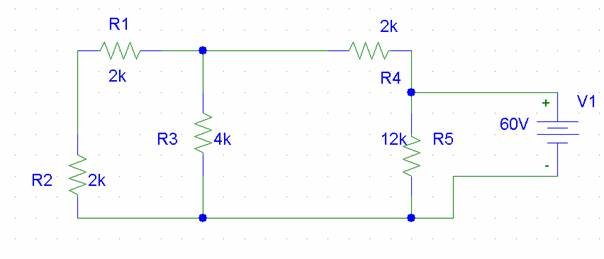
Çözüm:
Yukarıdaki devreyi sadeleştirirsek, R1 ile R2 seri bağlı oldukları için yerine tek bir direnç koyulduğunda:

(Devre2)
Şeklini alır. Yeni devredeki R1 ile R2 paraleldir o halde:
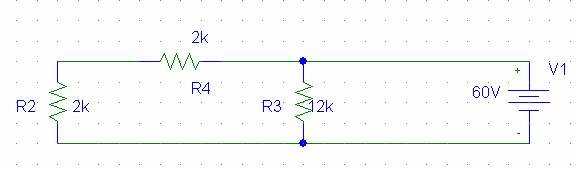
(Devre3)
Şeklinde tek bir direnç ile ifade edilebilir. Yeni devrede R2 ile R4 seridir o halde:
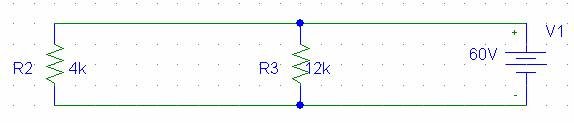
(Devre4)
Yukarıdaki devrenin son halinde R2 ile R3 paraleldir denilebilir. O halde devrede toplam direnç:

(Devre5)
3k olarak bulunur. Akım hesaplandığında toplam devrede akan akım 20amp olarak bulunur.
Paralel devreye (devre4) geri açılırsa r3 üzerindeki akım 5 amp , r2 üzerindeki akım ise 15 amp olarak hesaplanır.
Devre 4te bulunan R2 açılıp Devre 3 teki haline getirilirse, seri devrelerde akım aynı olacağı için, R4 üzerindeki gerilim farkı 30 V ve R2 üzerindeki gerilim farkı 30 V olacaktır.
R2 direnci açılıp Devre 2deki haline getirilirse, paralel devrelerdeki gerilim farkı aynı olacağı için, R1 üzerindeki akım 30/4, R2 üzerindeki akım da 30/4 olacaktır.
Son olarak devre orijinal haline getirildiğinde, R1 ve R2 dirençleri seri olduğu için akım aynı olacak ve üzerlerindeki gerilim farkı 15V olacaktır.
Tablo haline getirildiğinde:
|
|
R1 |
R2 |
R3 |
R4 |
R5 |
Rtoplam |
|
R |
2K |
2 K |
4 K |
2K |
12K |
3K |
|
I |
7,5mamp |
7,5mamp |
7,5mamp |
15mamp |
5mamp |
20mamp |
|
E |
15V |
15V |
30 |
30V |
60V |
60V |
A grubu Soru 1) Aşağıda verilen devreyi devre sadeleştirme metoduna göre çözüp her eleman üzerindeki gerilim, akım ve güç değerlerini bulunuz.

Çözüm: Yukarıdaki devrede bulunan kısa devre fazlalıklar çıkarıldığında aşağıdaki halini alır:

Yukarıdaki devre sadeleştirildiğinde aşağıdaki şekilde çizilmelidir:

Devre sadeleştirildiğinde (paralel devreler tek bir direnç olarak gösterildiğinde):

Seri dirençler birleştirilip tek direnç yapıldığında ise tek bir 75/4K değerinde direnç elde edilir:
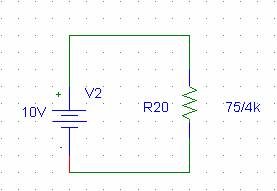
Bu devredeki akım 40/75 olarak bulunur.
Devre sadeleştirme metodu kullanılarak akım seri dirençler üzerine geri dağıtılırsa R14, R16, R17, R14 ve R9 üzerindeki akım aynı olur. Daha sonra devre ilk haline getirilerek paralel devreler üzerindeki gerilim farkları eşit düşünülürse, devrenin ilk halinde bulunan dirençler üzerindeki akım hesaplanabilir. Bu durumda değerler aşağıda verilmiştir:
|
|
R6 |
R7 |
R8 |
R9 |
R10 |
R11 |
R12 |
R13 |
Rtoplam |
|
E |
40/5V |
40/15 |
40/15 |
40/15V |
400/15V |
400/15V |
40/15V |
400/15V |
10V |
|
I |
40/15mamp |
30/15 |
10/15 |
40/15mamp |
400/450 |
400/450 |
40/15mamp |
400/450 |
40/15mamp |
|
R |
3K |
5K |
15K |
1K |
30K |
30K |
1K |
30K |
75/4K |
Soru 2) Aşağıda verilen devreyi sadeleştirip aynı x,y ve z girişi için aynı F sonucunu veren devreyi çiziniz:

Çözüm : Yukarıda verilen devrede en altta bulunan ve kapısının beslemelerinden y girişi kısa devre şeklinde olduğu için değil kapsını atlayabilir, sorunun çözümünde iki çözümü de doğru kabul ettim, iki çözümü de aşağıda veriyorum.
İlk çözüm (değil kapsını çalıştırırsak) Yukarıdaki devrede F sonucunu veren mantıksal önerme aşağıdaki şekilde yazılabilir:
xyz+xyz+xyz+xyz+xyz+xyz
yukarıdaki önerme veya kapılarında olumsuzluk alınarak tekrar olumsuzluğu alınmış önermedir. (olumsuzun olumsuzunun olumlu olduğunu hatırlayın).
Bu durumda ortak terimler tek terim ile ifade edilebilirse:
x'yz+xyz+xyz+xyz şeklinde yazılabilir. Karnough haritası çizilirse:
|
x\yz |
00 |
01 |
11 |
10 |
|
0 |
|
1 |
1 |
|
|
1 |
|
1 |
1 |
|
Şeklindeki harita elde edilmiş olur. Yukarıdaki haritada ortak terimler tek bir ada ile ifade edilebileceği için bu adayı veren önerme:
F=z terimidir. Bu terimin çizilmiş hali aşağıdadır:
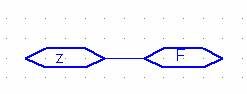
İkinci çözüm (şayet kapıyı kısa devre olarak düşünseydiniz).
xyz+xyz+xyz+xyz+xyz+xyz şeklinde önermeyi kabul etmeniz gerekirdi. Bu durumda ortak terimler toplandığında yine
x'yz+xyz+xyz+xyz şeklinde yazılabilir. Karnough haritası çizilirse:
|
x\yz |
00 |
01 |
11 |
10 |
|
0 |
|
1 |
1 |
|
|
1 |
|
1 |
1 |
|
Şeklindeki harita elde edilmiş olur. Yukarıdaki haritada ortak terimler tek bir ada ile ifade edilebileceği için bu adayı veren önerme:
F=z terimidir. Bu terimin çizilmiş hali aşağıdadır:

Soru 3) iki adet iki bitlik girişiniz olduğunu düşünün. İlk girişin ikinci girişten büyük olması durumunda 1, küçük veya eşit olması durumunda 0 döndüren devreyi tasarlayınız. (örneğin ilk giriş 10 ve ikinci giriş için 01 verilirse sonuç 0 olmalıdır)
Çözüm:
Girişleri ve sonuçları yazalım. İlk giriş değerine pq ikinci giriş değerine ise rs isimlerini verelim:
|
P |
Q |
R |
S |
F |
Karnough haritasındaki adresleri |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
2 |
|
0 |
0 |
1 |
1 |
0 |
3 |
|
0 |
1 |
0 |
0 |
1 |
4 |
|
0 |
1 |
0 |
1 |
0 |
5 |
|
0 |
1 |
1 |
0 |
0 |
6 |
|
0 |
1 |
1 |
1 |
0 |
7 |
|
1 |
0 |
0 |
0 |
1 |
8 |
|
1 |
0 |
0 |
1 |
1 |
9 |
|
1 |
0 |
1 |
0 |
0 |
10 |
|
1 |
0 |
1 |
1 |
0 |
11 |
|
1 |
1 |
0 |
0 |
1 |
12 |
|
1 |
1 |
0 |
1 |
1 |
13 |
|
1 |
1 |
1 |
0 |
1 |
14 |
|
1 |
1 |
1 |
1 |
0 |
15 |
Yukarıda bulduğumuz değerleri haritamıza yerleştirirsek:
|
PQ\RS |
00 |
01 |
11 |
10 |
|
00 |
|
|
|
|
|
01 |
1 |
|
|
|
|
11 |
1 |
1 |
|
|
|
10 |
1 |
1 |
|
1 |
Yukarıdaki haritayı elde etmiş oluruz. Bu haritada ortak terimler sadeleştirilecek olursa:
PR+QRS+PQS olarak bulunur. Bu önermenin devresi aşağıdaki şekildedir:
